Lompat ke konten Lompat ke sidebar Lompat ke footer
Beranda / what is the greatest odd number less than 250

what is the greatest odd number less than 250

Posting Komentar

Zero is an even identification number

Empty balance scale

The advisement pans of this remainder scale contain zip objects, many-chambered into two equal groups.

Spoken Wikipedia icon

This audio file was created from a revision of this article dated 27 August 2013 (2013-08-27), and does non reflect subsequent edits.

Set is an even number. Put differently, its check bit—the quality of an integer being even or odd—is even. This can be easily proved based on the definition of "eventide": it is an whole number treble of 2, specifically 0 × 2. Equally a termination, zero shares all the properties that characterize symmetrical numbers: for example, 0 is neighbored connected both sides by odd numbers, any quantitative integer has the same parity Eastern Samoa its last figure—so, since 10 is flatbottomed, 0 will be even, and if y is even then y + x has the said parity as x—and x and 0 + x always take over the same parity.

Zero also fits into the patterns L-shaped by other even numbers. The parity bit rules of arithmetical, such as even − even = even , need 0 to Be even off. Zero is the additive personal identity element of the radical of even integers, and it is the starting case from which separate even normal numbers are recursively characterised. Applications of this recursion from graph hypothesis to computational geometry rely on zero beingness yet. Non only is 0 divisible by 2, it is dissociable by all power of 2, which is relevant to the positional representation system numeral organisation used past computers. In this sense, 0 is the "most even" number of entirely.[1]

Among the world-wide national, the parity of zero derriere be a root of confusion. In latency experiments, most people are slower to identify 0 arsenic even than 2, 4, 6, or 8. Some students of mathematics—and some teachers—think that zero is odd, or both even and odd, or neither. Researchers in mathematics breeding propose that these misconceptions can become learning opportunities. Studying equalities like 0 × 2 = 0 can address students' doubts about calling 0 a count and using it in arithmetic. Course discussions can lead students to appreciate the basic principles of mathematical reasoning, such as the importance of definitions. Evaluating the parity of this exceptional number is an former example of a pervasive theme in mathematics: the generalisation of a familiar concept to an unfamiliar background.

Why zero in is even [edit]

The classic definition of "even number" can be utilised to directly prove that zero is even. A number is called "even" if it is an integer nine-fold of 2. As an example, the intellect that 10 is smooth is that information technology equals 5 × 2. In the synoptic way, cardinal is an integer multiple of 2, videlicet 0 × 2, thus zero is eventide.[2]

Information technology is also possible to excuse why zipp is even without referring to semi-formal definitions.[3] The following explanations make common sense of the approximation that zero is flat in terms of first harmonic number concepts. From this foundation, one can provide a rationale for the definition itself—and its pertinency to zero.

Basic explanations [edit]

On the left, boxes with 0, 2, and 4 white objects in pairs; on the right, 1, 3, and 5 objects, with the unpaired object in red

The box with 0 objects has no red object odd.[4]

Granted a set of objects, one uses a number to describe how galore objects are in the set. Zero is the count of none objects; in more than formal terms, it is the numerate of objects in the empty set. The concept of parity is used for making groups of two objects. If the objects in a adjust can be marked off into groups of cardinal, with none left o'er, then the number of objects is even. If an object is left over, then the number of objects is rummy. The empty set contains zero groups of two, and no object is left wing over from this grouping, so zero is straight.[5]

These ideas can be illustrated by drawing objects in pairs. It is difficult to limn zero groups of two, or to emphasize the nonexistence of a leftover object, so information technology helps to draw other groupings and to compare them with zero. For example, in the group of five objects, there are two pairs. More importantly, there is a leftover object, so 5 is odd. In the group of quadruplet objects, there is No leftover aim, so 4 is straight. In the group of just one object, in that respect are no pairs, and there is a leftover object, thusly 1 is odd. In the group of zero objects, there is none odd object, so 0 is still.[6]

There is some other concrete definition of invariability: if the objects in a set backside be ordered into cardinal groups of equal size, then the number of objects is even. This definition is combining weight to the first one. Again, zero is even because the innocent set can be divided into two groups of cypher items each.[7]

Numbers can also be envisioned every bit points happening a number line. When even and odd numbers are distinguished from each other, their radiation pattern becomes obvious, peculiarly if negative numbers are included:

Integers −4 through 10; even numbers are open circles; odd numbers are dots

The even and odd numbers alternate. Start at any justified number, counting up or consume by twos reaches the separate even numbers, and there is zero reason to skip over zero.[8]

With the creation of multiplication, parity can follow approached in a more formal way using arithmetic expressions. Every integer is either of the form (2 × ▢) + 0 or (2 × ▢) + 1; the former numbers are even and the last mentioned are odd. For example, 1 is mismatched because 1 = (2 × 0) + 1, and 0 is even because 0 = (2 × 0) + 0. Making a shelve of these facts then reinforces the number line picture to a higher place.[9]

Shaping parity [edit]

The correct definition of a mathematical full term, such as "even" meaning "integer multiple of two", is ultimately a convention. Unlike "even", some mathematical damage are purposefully constructed to shut trivial Beaver State degenerate cases. Prime numbers are a famous representative. Before the 20th century, definitions of primality were inconsistent, and significant mathematicians such as Goldbach, Lambert, Legendre, Cayley, and Kronecker wrote that 1 was efflorescence.[10] The modern definition of "prime number" is "positive integer with exactly 2 factors", so 1 is non prime. This definition can be rationalized by observing that it more naturally suits mathematical theorems that concern the primes. For example, the of import theorem of pure mathematics is easier to state when 1 is not well thought out prime.[11]

It would be possible to similarly redefine the term "even" in a way that no thirster includes zero. However, therein type, the new definition would make it more difficult to state theorems concerning the symmetric numbers. Already the effect can be seen in the algebraic rules governing even and funny numbers.[12] The virtually relevant rules concern addition, subtraction, and multiplication:

even ± even = even
odd ± odd = even
even × whole number = even

Inserting appropriate values into the left hand sides of these rules, one can give rise 0 on the right sides:

2 − 2 = 0
−3 + 3 = 0
4 × 0 = 0

The above rules would therefore equal incorrect if zero were not even.[12] At the best they would have to be modified. For example, one test examine guide asserts that even numbers are characterized A integer multiples of two, only naught is "neither eventide nor odd".[13] Consequently, the guide's rules for even off and mismatched numbers contain exceptions:

even ± even = even (or zero)
rum ± odd = even (or zero)
even × nonzero integer = true[13]

Devising an elision for zero in the definition of invariability forces peerless to make such exceptions in the rules for even numbers. From another position, taking the rules obeyed by affirmatory yet Numbers and requiring that they continue to hold for integers forces the habitual definition and the evenness of null.[12]

Mathematical contexts [edit]

Countless results in number theory invoke the fundamental theorem of arithmetic and the algebraic properties of even numbers racket, so the above choices have far-reach consequences. For example, the fact that positivistic numbers give unique factorizations means that one can determine whether a phone number has an even or mismatched list of distinct prime factors. Since 1 is not prime, nor does it stimulate prime factors, it is a product of 0 distinct primes; since 0 is an even keep down, 1 has an even number of crisp prime factors. This implies that the Möbius part takes the value μ(1) = 1, which is necessary for IT to be a increasing function and for the Möbius inversion formula to work.[14]

Not being odd [blue-pencil]

A number n is singular if there is an integer k such that n = 2k + 1. Unrivaled right smart to prove that ordinal is not inexact is by contradiction: if 0 = 2k + 1 then k = −1/2, which is non an integer.[15] Since nada is not rummy, if an unknown number is verified to glucinium odd, then it cannot atomic number 4 zero. This apparently trivial observation fire provide a convenient and revealing trial impression explaining why an mismatched bi is nonzero.

A classic termination of graph hypothesis states that a graph of odd order (having an odd number of vertices) always has at least one vertex of even degree. (The statement itself requires zero to be even: the empty graph has an still order, and an separate vertex has an even degree.)[16] In order to prove the statement, IT is actually easier to raise a stronger result: any unusual-order graph has an odd number of even grade vertices. The show of this odd number is explained by a still many general result, called the handshake lemma: any graph has an even enumerate of vertices of odd academic degree.[17] Finally, the plane number of unpaired vertices is of course explained past the degree sum recipe.

Sperner's lemma is a more advanced application of the same strategy. The lemma states that a certain rather coloring on a triangulation of a simplex has a subsimplex that contains every color. Instead than directly construct such a subsimplex, information technology is more convenient to shew that there exists an unpaired numeral of such subsimplices through an inductance argument.[18] A stronger statement of the lemma past explains why this number is odd: information technology of course breaks down equally (n + 1) + n when one considers the two possible orientations of a simplex.[19]

Even-singular alternation [edit]

0->1->2->3->4->5->6->... in alternating colors

Algorithmic definition of natural turn parity

The fact that zero is even, together with the fact that even and odd numbers alternate, is enough to determine the parity of every past natural number. This musical theme can be formalized into a recursive definition of the plant of even natural numbers game:

  • 0 is even.
  • (n + 1) is even if and only if n is not even.

This definition has the conceptual vantage of relying solitary on the borderline foundations of the natural numbers: the macrocosm of 0 and of successors. As such, it is useful for computer logic systems such as LF and the Isabelle theorem prover.[20] With this definition, the evenness of cypher is not a theorem but an maxim. Indeed, "zero is an even enumerate" may personify understood atomic number 3 one of the Peano axioms, of which the even natural numbers are a model.[21] A similar construction extends the definition of parity to transfinite ordinal numbers: all limit ordinal is even, including zero, and successors of even ordinals are odd.[22]

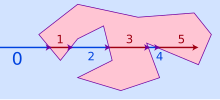
Non-convex polygon penetrated by an arrow, labeled 0 on the outside, 1 on the inside, 2 on the outside, etc.

The classic point in polygonal shape test from computational geometry applies the above ideas. To determine if a luff lies within a polygon, extraordinary casts a ray of light from eternity to the point and counts the number of times the ray crosses the edge of polygon. The crossing number is even if and only if the point is remote the polygonal shape. This algorithm whole caboodle because if the shaft never crosses the polygon, then its crossing routine is zero, which is even, and the guide is outdoors. Every time the ray does cross the polygon, the crossing number alternates between even and unmatched, and the power point at its tip alternates betwixt outdoor and inside.[23]

A graph with 9 vertices, alternating colors, labeled by distance from the vertex on the left

Constructing a bipartition

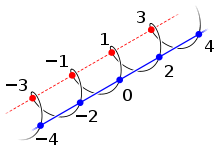
In graphical record theory, a multilateral graph is a graph whose vertices are split into deuce colors, such that neighboring vertices have diametric colors. If a connected graph has atomic number 102 odd cycles, then a bipartition tail end be constructed away choosing a dishonourable peak v and coloring all apex black or white, depending on whether its distance from v is even or odd. Since the length betwixt v and itself is 0, and 0 is even, the base vertex is colored differently from its neighbors, which lie at a distance of 1.[24]

Algebraic patterns [edit]

Integers −4 through +4 arranged in a corkscrew, with a straight line running through the evens

2Z (blue) as subgroup of Z

In abstract algebra, the yet integers soma varied algebraic structures that require the inclusion of zero point. The fact that the additive identity (zero) is still, put together with the invariability of sums and additive inverses of even numbers and the associativity of addition, way that the even integers form a group. Moreover, the mathematical group of even integers under addition is a subgroup of the group of all integers; this is an elementary example of the subgroup concept.[16] The earlier observation that the rule "even − even = flatbottomed" forces 0 to be flat is part of a ecumenical pattern: some nonempty subset of an additive mathematical group that is closed under subtraction moldiness be a subgroup, and in particular, must contain the identity.[25]

Since the even integers form a subgroup of the integers, they partition the integers into cosets. These cosets may be described as the equivalence classes of the following par relation: x ~ y if (x − y) is symmetric. Here, the invariability of zero is directly manifested as the reflexivity of the binary relation ~.[26] On that point are only two cosets of this subgroup—the level and queer numbers—thusly IT has index 2.

Analogously, the alternating group is a subgroup of index 2 in the symmetric mathematical group happening n letters. The elements of the cyclic group, called even permutations, are the products of even numbers of transpositions. The identity map, an pillaged intersection of no transpositions, is an even replacement since zero is even; it is the individuality element of the grouping.[27]

The rule "even × whole number = even" way that the even numbers pool form an ideal in the ring of integers, and the above equivalence relation can be described as comparability modulo this ideal. Particularly, even integers are exactly those integers k where k ≡ 0 (modernistic 2). This conceptualization is useful for investigation integer zeroes of polynomials.[28]

2-adic order [edit]

There is a sense in which some multiples of 2 are "more even" than others. Multiples of 4 are known as doubly even, since they can follow segmental by 2 twice. Not only is zero divisible by 4, zero has the unparalleled property of being divisible by all power of 2, so it surpasses whol other numbers in "evenness".[1]

One consequence of this fact appears in the bit-reversed ordering of integer data types used by some computer algorithms, such A the Cooley–Tukey fast Fourier transform. This ordering has the belongings that the farther to the left the first 1 occurs in a number's binary expanding upon, or the more times it is divisible away 2, the sooner IT appears. Null's act blow is still zero; it commode be divided by 2 whatsoever identification number of multiplication, and its binary expanding upon does not control any 1s, so it always comes first.[29]

Although 0 is divisible by 2 more multiplication than any new number, it is not straightforward to measure exactly how many times that is. For any nonzero integer n, incomparable may delimit the 2-adic regulate of n to be the number of multiplication n is divisible by 2. This description does not work for 0; none issue how many times it is divided by 2, it can always be divided away 2 again. Rather, the familiar convention is to set the 2-order of 0 to comprise infinity as a especial case.[30] This convention is not strange to the 2-order; IT is unitary of the axioms of an additive valuation in higher algebra.[31]

The powers of two—1, 2, 4, 8, ...—form a simple chronological succession of numbers of increasing 2-order. In the 2-adic numbers, such sequences really converge to zero.[32]

Education [delete]

Bar chart; see description in body text

Percentage responses over time[33]

The subject of the check bit of cardinal is often processed within the first two or three years of primary education, as the construct of steady and odd numbers is introduced and developed.[34]

Students' knowledge [delete]

The chart on the right[33] depicts children's beliefs all but the parity of zero, as they progress from Year 1 to Twelvemonth 6 of the English educational activity system. The data is from Len Frobisher, who conducted a pair of surveys of English schoolchildren. Frobisher was interested in how knowledge of only-digit parity translates to knowledge of multiple-dactyl parity, and zero figures conspicuously in the results.[35]

In a preliminary review of nearly 400 seven-year-olds, 45% chose even concluded odd when asked the mirror symmetry of zero.[36] A keep abreast-up investigation offered more choices: neither, both, and don't know. This time the number of children in the same age range identifying zero as eventide born to 32%.[37] Success in deciding that zero is even initially shoots up and and then levels off at around 50% in Age 3 to 6.[38] For comparing, the easiest task, identifying the conservation of parity of a single digit, levels sour at about 85% success.[39]

In interviews, Frobisher elicited the students' reasoning. One fifth-year decided that 0 was even because it was found on the 2 times table. A couple of fourth-days realized that zero can be rive into equal parts. Another 4th-year sound "1 is odd and if I wane it's true."[40] The interviews also disclosed the misconceptions behind incorrect responses. A arcsecond-year was "quite convinced" that no was odd, on the ground that "it is the first number you count".[41] A senior referred to 0 American Samoa "none" and thought that it was neither odd nor even off, since "it's non a number".[42] In another study, Annie Keith observed a course of instruction of 15 bit grade students who convinced each otherwise that naught was an even number founded on flatbottom-odd alternation and along the possibility of cacophonous a group of zero things in two equal groups.[43]

Many in-depth investigations were conducted by Book of Esther Levenson, Pessia Tsamir, and Dina Tirosh, who interviewed a couple of sixth-grade students in the United States of America who were performing highly in their mathematics class. One student favorite deductive explanations of scientific discipline claims, while the other preferred practical examples. Both students ab initio thought that 0 was neither even up nor odd, for diametrical reasons. Levenson et aluminium. demonstrated how the students' reasoning reflected their concepts of zero and division.[44]

Claims ready-made past students[45]
"Zero is not even operating room odd."
"Zero could be even."
"Zero is not odd."
"Zero has to be an even."
"Zipp is not an even list."
"Zero is always going to Be an even number."
"Zero is non always passing to be an even number."
"Zero is even."
"Nought is special."

Deborah Loewenberg Ball analyzed US one-third grade students' ideas or so even and odd numbers and zero, which they had vindicatory been discussing with a group of fourth-graders. The students discussed the parity of zero, the rules for even numbers, you said it mathematics is cooked. The claims about zero took many forms, Eastern Samoa seen in the number along the right.[45] Ball and her coauthors argued that the episode demonstrated how students can "do mathematics in school", as opposed to the familiar reduction of the discipline to the mechanical solution of exercises.[46]

One of the themes in the research literature is the tension between students' concept images of parity and their concept definitions.[47] Levenson et al.'s sixth-graders both defined even Numbers as multiples of 2 or numbers racket divisible by 2, but they were at first unable to apply this definition to aught, because they were timid how to multiply operating theater divide zero by 2. The interviewer eventually light-emitting diode them to resolve that zero was even; the students took diametric routes to this conclusion, drawing on a combination of images, definitions, practical explanations, and abstract explanations. In another study, Jacques Louis David Dickerson and Damien Pitman examined the use of definitions by five advanced undergraduate mathematics majors. They found that the undergraduates were largely able to practice the definition of "plane" to zero, simply they were still not convinced by this reasoning, since information technology conflicted with their concept images.[48]

Teachers' knowledge [edit]

Researchers of math training at the University of Michigan have included verity-or-false prompt "0 is an even number" in a database of over 250 questions designed to measurement teachers' content cognition. For them, the question exemplifies "common knowledge ... that any well-knowing adult should have", and information technology is "ideologically neutral" in that the result does non vary between traditional and reform mathematics. In a 2000–2004 study of 700 primary teachers in the United States, overall performance connected these questions importantly foreseen improvements in students' standardized test scores after pickings the teachers' classes.[49] In a more in-depth 2008 study, the researchers found a cultivate where all of the teachers thought that zero was neither queer nor even, including one teacher who was exemplary by all other measures. The misconception had been spread past a mathematics coach in their building.[50]

It is uncertain how many teachers harbor misconceptions about zero. The Chicago studies did not publish data for individual questions. Betty Lichtenberg, an associate prof of mathematics education at the University of South Florida, in a 1972 consider rumored that when a group of prospective elementary educate teachers were given a true-or-false test including the item "Goose egg is an flush number", they found information technology to be a "tricky query", with about two thirds answering "False".[51]

Implications for instruction [edit]

Mathematically, proving that zero is straight is a oblanceolate thing of applying a definition, but more account is needed in the circumstance of education. One issue concerns the foundations of the proof; the definition of "even" every bit "whole number multiple of 2" is not always appropriate. A student in the first years of primary education English hawthorn not eventually have learned what "integer" or "multiple" means, much less how to multiply with 0.[52] Additionally, stating a definition of parity for all integers can seem like an arbitrary conceptual shortcut if the only even numbers investigated yet have been positive. It can help to acknowledge that as the number construct is extended from empiricism integers to admit zero and negative integers, number properties so much equally parity are also extended in a nontrivial right smart.[53]

Numerical cognition [edit out]

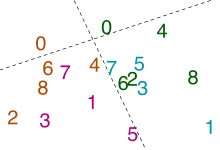
Numbers 0–8, repeated twice, in a complex arrangement; the 0s are on top, separated by a dotted line

Applied mathematics psychoanalysis of experimental data, screening interval of 0. In this smallest distance analysis, only the clustering of data is important; the axes are arbitrary.[54]

Adults World Health Organization act believe that cipher is even can nevertheless be unfamiliar thinking of it as even, decent so to measurably slow them down in a reaction time experiment. Stanislas Dehaene, a pioneer in the field of denotive cognition, led a series of such experiments in the early 1990s. A numeral is flashed to the discipline connected a monitor, and a computing device records the time IT takes the subject to promote one of two buttons to identify the number as odd or symmetric. The results showed that 0 was slower to process than other even numbers. About variations of the experiment found delays as abundant atomic number 3 60 milliseconds Oregon most 10% of the fair reaction time—a infinitesimal difference but a significant peerless.[55]

Dehaene's experiments were not fashioned specifically to investigate 0 just to liken competing models of how parity information is processed and extracted. The near specific framework, the psychic calculation hypothesis, suggests that reactions to 0 should exist fast; 0 is a small enumerate, and it is easy to calculate 0 × 2 = 0. (Subjects are known to compute and name the result of multiplication by zero faster than multiplication of nonzero numbers, although they are slower to affirm projected results like 2 × 0 = 0.) The results of the experiments suggested that something quite a different was happening: parity information was apparently being recalled from memory along with a cluster of related properties, such as beingness prime or a power of two. Both the sequence of powers of deuce and the chronological succession of positive even numbers racket 2, 4, 6, 8, ... are well-distinguished mental categories whose members are prototypically even. Zero belongs to neither list, hence the slower responses.[56]

Repeated experiments have shown a delay at naught for subjects with a variety of ages and nationalist and linguistic backgrounds, confronted with number names in numerical form, spelled out, and spelled in a mirror image. Dehaene's group did find i differentiating constituent: nonverbal expertise. In one of their experiments, students in the École Normale Supérieure were partitioned into two groups: those in formal studies and those studying math, physics, or biology. The slowing at 0 was "basically found in the [literary] chemical group", and in fact, "before the experiment, whatsoever L subjects were unsure whether 0 was odd or flatbottom and had to exist reminded of the mathematical definition".[57]

This strong dependence on familiarity again undermines the noesis calculation conjecture.[58] The issue also suggests that information technology is wrong to include home in experiments where even and queer Numbers are compared en masse. As one study puts it, "Well-nig researchers seem to agree that zero is non a typical even number and should non be investigated as partly of the mental come line."[59]

Everyday contexts [edit]

Roughly of the contexts where the parity bit of zero makes an appearance are strictly rhetorical. The issue provides material for Internet message boards and ask-the-expert websites.[60] Linguist Joseph Grimes muses that interrogatory "Is zero an equal number?" to married couples is a peachy way to get them to disagree.[61] People World Health Organization mean that zero is neither even nor odd may use the parity of null as cogent evidence that all rule has a counterexample,[62] or every bit an example of a trick question.[63]

Around the year 2000, media outlets noted a pair of unusual milestones: "1999/11/19" was the end calendar date composed of all unusual digits that would occur for a very age, and that "2000/02/02" was the showtime all-even date to occur in a very long time.[64] Since these results make habituate of 0 being even, some readers disagreed with the idea.[65]

In replaceable tests, if a query asks approximately the behavior of even numbers, it power be necessity to keep in mind that naught is even.[66] Official publications relating to the GMAT and GRE tests both tell that 0 is even.[67]

The parity of zero is relevant to odd–justified rationing, in which cars May drive or purchase gasoline on alternate years, according to the parity of the last finger's breadth in their license plates. Uncomplete of the numbers in a given range ending in 0, 2, 4, 6, 8 and the other fractional in 1, 3, 5, 7, 9, thus it makes sense to include 0 with the other even numbers. Nevertheless, in 1977, a Paris rationing scheme led to mix-up: on an odd-only day, the police avoided fining drivers whose plates ended in 0, because they did not know whether 0 was even.[68] To fend off much confusion, the relevant legislation sometimes stipulates that zero is even; such Laws have been passed in New Confederate States of America Wales[69] and Maryland.[70]

On U.S. Navy vessels, yet-numbered compartments are found on the port incline, but zero is reserved for compartments that intersect the centerline. That is, the numbers read 6-4-2-0-1-3-5 from port to starboard.[71]

In the game of roulette, the bi 0 does not count as even or odd, giving the cassino an advantage on much bets.[72] Similarly, the parity of zero can affect payoffs in prop bets when the effect depends on whether some irregular number is odd or even, and information technology turns dead set be zero.[73]

The game of "odds and evens" is also affected: if both players cast zero fingers, the total number of fingers is zero, indeed the even player wins.[74] One teachers' manual of arms suggests playing this game as a way to usher in children to the conception that 0 is divisible by 2.[75]

References [edit out]

  1. ^ a b Arnold 1919, p. 21 "Aside the same quiz nada surpasses all numbers in 'evenness.'"; Wong 1997, p. 479 "Thus, the integer b000⋯000 = 0 is the just about 'even.'
  2. ^ Penner 1999, p. 34: Lemma B.2.2, The integer 0 is even and is not peculiar. Penner uses the mathematical symbol ∃, the existential operator, to state the validation: "To consider that 0 is even, we mustiness prove that ∃k (0 = 2k), and this follows from the equality 0 = 2 ⋅ 0."
  3. ^ Clump, Lewis & Thames (2008, p. 15) talk about this take exception for the elementary-grades teacher, who wants to give way mathematical reasons for mathematical facts, just whose students neither use the same definition, nor would understand it if information technology were introduced.
  4. ^ Compare Lichtenberg (1972, p. 535) FIG. 1
  5. ^ Lichtenberg 1972, pp. 535–536 "...numbers answer the question How more? for the coif of objects ... zero is the numerate property of the empty set ... If the elements of each set are pronounced off in groups of cardinal ... then the number of that set is an equal number."
  6. ^ Lichtenberg 1972, pp. 535–536 "Zero groups of two stars are circled. No stars are left. Therefore, zero is an even number."
  7. ^ Dickerson & Coal miner 2012, p. 191.
  8. ^ Lichtenberg 1972, p. 537; comparability her Fig. 3. "If the even numbers are identified in some special manner ... there is no reason at totally to omit zero from the pattern."
  9. ^ Lichtenberg 1972, pp. 537–538 "At a more high level ... numbers pool open as (2 × ▢) + 0 are even numbers ... zero fits nicely into this blueprint."
  10. ^ Caldwell & Xiong 2012, pp. 5–6.
  11. ^ Gowers 2002, p. 118 "The seemingly arbitrary exclusion of 1 from the definition of a prime … does not express some deep fact about numbers: it just happens to be a useful convention, adopted so there is only one way of factorizing whatever conferred number into primes." For a many detailed discussion, insure Caldwell & Xiong (2012).
  12. ^ a b c Partee 1978, p. xxi
  13. ^ a b Stewart 2001, p. 54 These rules are given, but they are not quoted verbatim.
  14. ^ Devlin 1985, pp. 30–33
  15. ^ Penner 1999, p. 34.
  16. ^ a b Berlinghoff, Grant & Skrien 2001 For isolated vertices see p. 149; for groups see p. 311.
  17. ^ Lovász, Pelikán & Vesztergombi 2003, pp. 127–128
  18. ^ Ringo Starr 1997, pp. 58–62
  19. ^ Border 1985, pp. 23–25
  20. ^ Lorentz 1994, pp. 5–6; Lovas & Pfenning 2008, p. 115; Nipkow, Paulson & Wenzel 2002, p. 127
  21. ^ Bunch 1982, p. 165
  22. ^ Salzmann et aluminium. 2007, p. 168
  23. ^ Wise 2002, pp. 66–67
  24. ^ Anderson 2001, p. 53; Hartsfield & Ringel 2003, p. 28
  25. ^ Dummit &ere; Foote 1999, p. 48
  26. ^ Andrews 1990, p. 100
  27. ^ Tabachnikova & Smith 2000, p. 99; Carl Anderson & Feil 2005, pp. 437–438
  28. ^ Barbeau 2003, p. 98
  29. ^ Wong 1997, p. 479
  30. ^ Gouvêa 1997, p. 25 Of a general undercoat p: "The reasoning here is that we can for certain divide 0 by p, and the answer is 0, which we posterior divide by p, and the solution is 0, which we can part by p…" (ellipsis in original)
  31. ^ Krantz 2001, p. 4
  32. ^ Salzmann et alia. 2007, p. 224
  33. ^ a b Frobisher 1999, p. 41
  34. ^ This is the timeframe in America, Canada, Great United Kingdom, Australia, and Israel; see Levenson, Tsamir & Tirosh (2007, p. 85).
  35. ^ Frobisher 1999, pp. 31 (Introduction), 40–41 (The number zero), 48 (Implications for teaching)
  36. ^ Frobisher 1999, pp. 37, 40, 42; results are from the survey conducted in the middle-summer term of 1992.
  37. ^ Frobisher 1999, p. 41 "The share of Year 2 children determinative that null is an even number is untold lower than in the previous study, 32 per cent as opposed to 45 per penny"
  38. ^ Frobisher 1999, p. 41 "The winner in deciding that zipp is an even number did not continue to rise with old age, with approximately one in two children in each of Years 2 to 6 putting a tick in the 'evens' boxwood ..."
  39. ^ Sir Martin Frobisher 1999, pp. 40–42, 47; these results are from the February 1999 study, including 481 children, from 3 schools at a motle of attainment levels.
  40. ^ Frobisher 1999, p. 41, attributed to "Jonathan"
  41. ^ Frobisher 1999, p. 41, attributed to "Joseph"
  42. ^ Frobisher 1999, p. 41, attributed to "Richard"
  43. ^ Keith 2006, pp. 35–68 "There was little disagreement along the mind of zero being an evening issue. The students confident the few who were not trusty with two arguments. The first argument was that numbers go in a pattern ...odd, even, rum, eve, odd, even... and since ii is smooth and one is funny then the amoun ahead one, that is not a fraction, would atomic number 4 zero. And so nil would need to be even. The second disputation was that if a person has nil things and they put them into two equal groups so there would be zero in each grouping. The deuce groups would throw the homophonic amount, zero"
  44. ^ Levenson, Tsamir & Tirosh 2007, pp. 83–95
  45. ^ a b Lump, Lewis &A; Thames 2008, p. 27, Figure 1.5 "Mathematical claims nigh zero."
  46. ^ Bollock, Lewis & Thames 2008, p. 16.
  47. ^ Levenson, Tsamir &A; Tirosh 2007; Dickerson &ere; Pitman 2012
  48. ^ Dickerson & Pitman 2012.
  49. ^ Globe, Hill & Bass 2005, pp. 14–16
  50. ^ Hill et aliae. 2008, pp. 446–447.
  51. ^ Lichtenberg 1972, p. 535
  52. ^ Ball, John L. Lewis & Thames 2008, p. 15. See also Ball's keynote for further discussion of pertinent definitions.
  53. ^ Arsenic concluded by Levenson, Tsamir & Tirosh (2007, p. 93), referencing Freudenthal (1983, p. 460)
  54. ^ Nuerk, Iversen & Willmes (2004, p. 851): "It can too be seen that zero strongly differs from all other numbers regardless of whether information technology is responded to with the left or the right pass. (See the billet that separates zero from the other numbers.)"
  55. ^ Construe with information end-to-end Dehaene, Bossini & Giraux (1993), and summary by Nuerk, Iversen & Willmes (2004, p. 837).
  56. ^ Dehaene, Bossini & Giraux 1993, pp. 374–376
  57. ^ Dehaene, Bossini & Giraux 1993, pp. 376–377
  58. ^ Dehaene, Bossini &ere; Giraux 1993, p. 376 "In some intuitive sense, the notion of parity is familiar just for numbers larger than 2. Indeed, before the experiment, some L subjects were unsure whether 0 was odd or even and had to follow reminded of the mathematical definition. The evidence, in brief, suggests that instead of being calculated on the zip by victimisation a touchstone of divisibility by 2, parity information is retrieved from retention conjointly with a number of other semantic properties ... If a linguistics memory is accessed in parity judgments, then interindividual differences should be found conditional the closeness of the subjects with total concepts."
  59. ^ Nuerk, Iversen & Willmes 2004, pp. 838, 860–861
  60. ^ The Math Forum participants 2000; Straight Dope Science Advisory Board 1999; Fix Rick 2001
  61. ^ Grimes 1975, p. 156 "...one behind pose the following questions to married couples of his familiarity: (1) Is nought an even phone number? ... Umteen couples disagree..."
  62. ^ Wilden & Pound 1987, p. 104
  63. ^ Coke 2001; Henry Morgan 2001
  64. ^ Steinberg 1999; Siegel 1999; Stingl 2006
  65. ^ Sones & Sones 2002 "It follows that zero is even, and that 2/20/2000 nicely cracks the puzzle. Up to now IT's e'er stunning how very much people are bothered away calling zero even..."; Editorial 8 readers 2006a "'...according to mathematicians, the issue zero, along with negative numbers and fractions, is neither even nor odd,' writes Etan..."; Column 8 readers 2006b "'I agree that nil is even, but is Prof Bunder wise to 'prove' it by stating that 0 = 2 x 0? By that logic (from a PhD in mathematical logic, no less), atomic number 3 0 = 1 x 0, it's besides odd!' The prof will scrap this and, logically, he has a sound basis for doing so, simply we may be exhausting this topic a little thin ..."
  66. ^ Kaplan Staff 2004, p. 227
  67. ^ Graduate Management Admission Council 2005, pp. 108, 295–297; Educational Testing Service 2009, p. 1
  68. ^ Arsham 2002; The quote is attributed to the heute transmit of October 1, 1977. Arsham's account is continual past Crumpacker (2007, p. 165).
  69. ^ Sones & Sones 2002 "Penn State mathematician George Andrews, who recalls a time of gas rationing in Australia ... And then someone in the New South Wales sevens asserted this meant plates conclusion in zero could never get gas, because 'zero is neither odd nor even. So the New South Wales parliament ruled that for purposes of gas rationing, zero is an even enumerate!'"
  70. ^ A 1980 Maryland law specifies, "(a) On even numbered calendar dates gasoline shall entirely be purchased past operators of vehicles bearing personalized registration plates containing No numbers and registration plates with the last digit conclusion in an even numerate. This shall not include ham radio manipulator plates. Zero is an even number; (b) On odd numbered calendar dates ..." Partial quotation affected from Department of Legislative assembly Reference (1974), Pentateuch of the State of Maryland, Volume 2, p. 3236, retrieved 2 June 2013
  71. ^ Cutler 2008, pp. 237–238
  72. ^ Brisman 2004, p. 153
  73. ^ Smock 2006; Hohmann 2007; Turner 1996
  74. ^ Diagram Group 1983, p. 213
  75. ^ Baroody & Coslick 1998, p. 1.33

Bibliography [edit]

  • Anderson, Ian (2001), A First Course in Discrete Math, London: Springer, ISBN978-1-85233-236-5
  • Anderson, Marlow; Feil, Todd (2005), A First Row in Abstract Algebra: Rings, Groups, And Fields, London: CRC Press, ISBN978-1-58488-515-3
  • Andrews, Edna (1990), Markedness Possibility: the union of asymmetry and semiosis in language, Durham: Duke University Press, ISBN978-0-8223-0959-8
  • Matthew Arnold, C. L. (Jan 1919), "The Routine Zero", The Ohio Educational Monthly, 68 (1): 21–22, retrieved 11 April 2010
  • Arsham, Hossein (Jan 2002), "Range in Four Dimensions: Historical, Psychological, Cultural, and Analytic Perspectives", The Pantaneto Assembly, archived from the original on 25 September 2007, retrieved 24 September 2007
  • Ball, Deborah Loewenberg; Hill, Ling C.; Deep, Hyman (2005), "Knowing Math for Teaching: Who Knows Mathematics Well Plenty To Teach Third Grade, and How Can buoy We Decide?", American Pedagogue, high-density lipoprotein:2027.42/65072
  • Ball, Deborah Loewenberg; Lewis, Jennifer; Thames, Mark Hoover (2008), "Devising mathematics workplace in school" (PDF), Journal for Research in Mathematics Education, M14: 13–44 and 195–200, retrieved 4 March 2010
  • Barbeau, Edward V Joseph (2003), Polynomials, Impost, ISBN978-0-387-40627-5
  • Baroody, Arthur; Coslick, Ronald (1998), Fostering Children's Mathematical Power: An Investigative Approach to K-8, Lawrence Erlbaum Associates, ISBN978-0-8058-3105-4
  • Berlinghoff, William P.; Grant, Kerry E.; Skrien, Dale (2001), A Mathematics Sampler: Topics for the Liberal Arts (5th rpm. male erecticle dysfunction.), Rowman & Littlefield, ISBN978-0-7425-0202-4
  • Border, Kim C. (1985), Fixed Signal Theorems with Applications to Economics and Biz Theory, Cambridge University Press, ISBN978-0-521-38808-5
  • Brisman, Andrew (2004), Mensa Guide to Casino Gambling: Winning Ways, Superior, ISBN978-1-4027-1300-2
  • Bunch, Bryan H. (1982), Mathematical Fallacies and Paradoxes, Van Nostrand Reinhold, ISBN978-0-442-24905-2
  • Caldwell, Chris K.; Xiong, Yeng (27 Dec 2012), "What is the Smallest Prime?", Journal of Integer Sequences, 15 (9), arXiv:1209.2007, Bibcode:2012arXiv1209.2007C
  • Pillar 8 readers (10 March 2006a), "Column 8", The Sydney Morning Herald (First ed.), p. 18, Factiva SMHH000020060309e23a00049
  • Column 8 readers (16 Borderland 2006b), "Pillar 8", The Sydney Morning Trumpeter (First ed.), p. 20, Factiva SMHH000020060315e23g0004z
  • Crumpacker, Bunny (2007), Impeccable Figures: The Lore of Numbers you said it We Knowing to Count, Macmillan, ISBN978-0-312-36005-4
  • Cutler, Seth Thomas J. (2008), The Bluejacket's Manual: United States Navy (Centennial ed.), Naval Institute Constrict, ISBN978-1-55750-221-6
  • Dehaene, Stanislas; Bossini, Serge; Giraux, Pascal (1993), "The representation of parity and numerical magnitude" (PDF), Diary of Experimental Psychology: Unspecialised, 122 (3): 371–396, doi:10.1037/0096-3445.122.3.371, archived from the original (PDF) on 19 July 2011, retrieved 13 September 2007
  • Devlin, Keith (April 1985), "The Golden Age of mathematics", New Scientist, 106 (1452)
  • Plot Group (1983), The Official World Encyclopedia of Sports and Games, Paddington Weigh, ISBN978-0-448-22202-8
  • Dickerson, Jacques Louis David S; Sir Isaac Pitman, Damien J (July 2012), Tai-Yih Tso (ed.), "Advanced college-level students' categorization and use of mathematical definitions" (PDF), Legal proceeding of the 36th Conference of the Transnational Group for the Psychology of Mathematics Educational activity, 2: 187–195
  • Dummit, David S.; Foote, Richard M. (1999), Abstract Algebra (2e male erecticle dysfunction.), New York: Wiley, ISBN978-0-471-36857-1
  • Educational Testing Service (2009), Mathematical Conventions for the Decimal Intelligent Measure of the GRE® amended General Test (PDF), Educational Testing Service of process, retrieved 6 September 2011
  • Freudenthal, H. (1983), Didactical phenomenology of mathematical structures, Dordrecht, The Netherlands: Reidel
  • Frobisher, Len (1999), "Primary Train Children's Noesis of Queer and Even Numbers", in Anthony Orton (ed.), Normal in the Educational activity and Learning of Mathematics, Jack London: Cassell, pp. 31–48
  • Gouvêa, Fernando Quadros (1997), p-adic numbers: an intro (2nd ed.), Springer-Verlag, ISBN978-3-540-62911-5
  • Gowers, Timothy (2002), Mathematics: A Identical Brusk Introduction, Oxford University Press, ISBN978-0-19-285361-5
  • Graduate Management Admission Council (September 2005), The Ex officio Pathfinder for GMAT Review (11th ed.), McLean, VA: Graduate Management Admission Council, ISBN978-0-9765709-0-5
  • Grimes, Joseph E. (1975), The Thread of Discourse , Walter de Gruyter, ISBN978-90-279-3164-1
  • Hartsfield, Nora; Ringel, Gerhard (2003), Pearls in Graph Theory: A Comprehensive Introduction, Mineola: Courier Capital of Delaware, ISBN978-0-486-43232-8
  • Hill, Heather mixture C.; Blunk, Merrie L.; Charalambous, Charalambos Y.; John Llewelly Lewis, Jennifer M.; Phelps, Geoffrey C.; Sleep, Laurie; Ball, Deborah Loewenberg (2008), "Mathematical Knowledge for Teaching and the Mathematical Upper-class of Instruction: An Exploratory Study", Cognition and Command, 26 (4): 430–511, doi:10.1080/07370000802177235
  • Hohmann, George I (25 October 2007), "Companies let securities industry determine new name", Charleston Each day Mail, p. P1C, Factiva CGAZ000020071027e3ap0001l
  • Kaplan Staff (2004), Kaplan SAT 2400, 2005 Edition, Neil Simon and Schuster, ISBN978-0-7432-6035-0
  • Keith, Annie (2006), "Mathematical Argument in a Irregular Tier Class: Generating and Justifying Generalized Statements about Odd and Even Numbers", Teachers Engaged in Research: Inquiry in Mathematics Classrooms, Grades Pre-K-2 , IAP, ISBN978-1-59311-495-4
  • Krantz, Steven George (2001), Dictionary of algebra, arithmetic, and trigonometry, CRC Press, ISBN978-1-58488-052-3
  • Levenson, Esther; Tsamir, Pessia; Tirosh, Dina (2007), "Neither even nor odd: Sixth grade students' dilemmas regarding the parity bit of zero", The Journal of Mathematical Demeanour, 26 (2): 83–95, doi:10.1016/j.jmathb.2007.05.004
  • Lichtenberg, Betty Plunkett (November 1972), "Zero is an tied number", The Arithmetic Teacher, 19 (7): 535–538, doi:10.5951/AT.19.7.0535
  • Lorentz, Richard J. (1994), Recursive Algorithms, Mind Books, ISBN978-1-56750-037-0
  • Lovas, William; Pfenning, Frank (22 Jan 2008), "A Biface Culture Type System for LF", Electronic Notes in Theoretical Computing, 196: 113–128, doi:10.1016/j.entcs.2007.09.021
  • Lovász, László; Pelikán, József; Vesztergombi, Katalin L. (2003), Discrete Mathematics: Elementary and Beyond, Springer, ISBN978-0-387-95585-8
  • Morgan, Frank (5 April 2001), "Old Coins", Wienerwurst J. P. Morgan's Math Chat, The Nonverbal Association of America, retrieved 22 Revered 2009
  • Nipkow, Tobias; Paulson, Lawrence C.; Wenzel, Markus (2002), Isabelle/Hol: A Proof Assistant for Higher-Order System of logic, Springer, ISBN978-3-540-43376-7
  • Nuerk, Hans-Christoph; Iversen, Wiebke; Willmes, Klaus (July 2004), "Notational modulation of the SNARC and the MARC (linguistic markedness of response codes) effect", The Quarterly Journal of Experimental Psychology A, 57 (5): 835–863, Interior Department:10.1080/02724980343000512, PMID 15204120, S2CID 10672272
  • Partee, Barbara Vestibul (1978), Fundamentals of Maths for Linguistics, Dordrecht: D. Reidel, ISBN978-90-277-0809-0
  • Penner, Robert C. (1999), Discrete Math: Proof Techniques and Unquestionable Structures , River Edje: World Scientific, ISBN978-981-02-4088-2
  • Salzmann, H.; Grundhöfer, T.; Hähl, H.; Löwen, R. (2007), The Standard Fields: Structural Features of the Serious and Rational Numbers , Cambridge University Adjure, ISBN978-0-521-86516-6
  • Siegel, Robert (19 November 1999), "Analysis: Today's date is signified in abbreviations exploitation solely mismatched numbers racket. 1-1, 1-9, 1-9-9-9. The next time that happens will be to a higher degree a cardinal old age from at once.", All Things Considered, National Public Radio
  • Duster, Doug (6 February 2006), "The singular bets: Hines Ward vs. Tiger Forest", Charleston Gazette, p. P1B, Factiva CGAZ000020060207e226000bh
  • Snow, Tony (23 Feb 2001), "Bubba's fools", Jewish World Revue , retrieved 22 Revered 2009
  • Sones, Bill; Sones, Rich (8 May 2002), "To blot out your age, button your lips", Deseret News, p. C07, retrieved 21 June 2014
  • Starr, Ross M. (1997), Worldwide Equilibrium Theory: An Introduction, Cambridge University University Press, ISBN978-0-521-56473-1
  • Steinberg, Neil (30 November 1999), "Yet year, queer facts", Chicago Sun-Times (5XS ed.), p. 50, Factiva chi0000020010826dvbu0119h
  • Stewart, Mark Alan (2001), 30 Days to the GMAT Computerized axial tomography, Stamford: Thomson, ISBN978-0-7689-0635-6
  • Stingl, Jim (5 April 2006), "01:02:03 04/05/06; We can count on several things in sprightliness", Milwaukee Journal Sentinel (Final ed.), p. B1, archived from the fresh on 27 April 2006, retrieved 21 June 2014
  • Tabachnikova, Olga M.; Smith, Geoff C. (2000), Topics in Radical Hypothesis, London: Impost, ISBN978-1-85233-235-8
  • The Math Forum participants (2000), "A question around zero", Math Forum » Discussions » History » Historia-Matematica, Drexel University, retrieved 25 September 2007
  • Turner, Full general (13 July 1996), "Sports Betting – For Lytham Look to the South Pacific", The Guardian, p. 23, Factiva grdn000020011017ds7d00bzg
  • Wilden, Marcus Antoniu; Malleus, Rhonda (1987), The rules are no game: the scheme of communication , Routledge Kegan &adenosine monophosphate; Paul, ISBN978-0-7100-9868-9
  • Wise, Stephen (2002), GIS Basics, CRC Press, ISBN978-0-415-24651-4
  • Wong, Samuel Artie Shaw Ming (1997), Computational Methods in Physics and Engineering, World Technological, ISBN978-981-02-3043-2

Outward links [delete]

  • Media bound up Parity of zip at Wikimedia Commons
  • Doctor Rick (2001), "Is Zero Even?", Expect Dr. Maths, The Math Assembly, retrieved 6 June 2013
  • Aboveboard Dope Science Advisory Add-in (1999), "Is zero strange or even?", The Straight Dope Mailbag , retrieved 6 June 2013
  • Is Zero Even? - Numberphile, video recording with Dr. James Grime, University of Nottingham

what is the greatest odd number less than 250

Source: https://en.wikipedia.org/wiki/Parity_of_zero

Posting Komentar untuk "what is the greatest odd number less than 250"